|
|
||
|---|---|---|
| assets | ||
| docs/html | ||
| examples | ||
| ext | ||
| gui | ||
| include | ||
| src | ||
| tests | ||
| .gitignore | ||
| CMakeLists.txt | ||
| Doxyfile | ||
| LICENSE.txt | ||
| README.md | ||
README.md
3D linear beam element code
Getting started
This project requires CMake to compile the code. If not installed,
please install CMake before continuing. If you intend on building the
GUI, Qt must be installed and the path to the Qt5WidgetsConfig.cmake
file must be set when invoking CMake. Currently, the following method of
building the GUI works on Mac and Linux. If running on Windows, open the
fea_gui.pro file with QtCreator (included with the Qt installation) and
run. Alternatively, I can package pre-built binaries if there is
interest. #### To compile the code: #### 1. Open the
threed-beam-fea directory 2. Create a folder named
build 3. Open a terminal and navigate to the newly formed
build directory 4. Execute cmake .. * Use
-DCMAKE_BUILD_TYPE=debug if you would like to build the
code for debugging purposes. By default the make files will be
configured for the release build. * If you wish to build the GUI execute
cmake .. -DFEA_BUILD_GUI=ON -DCMAKE_PREFIX_PATH="/path/to/Qt"
- This requires you have Qt >= 5.0 installed. -
-DFEA_BUILD_GUI=ON tells cmake to add the
../gui subdirectory and adds fea_gui to the
targets. - -DCMAKE_PREFIX_PATH="/path/to/Qt" should be the
path to the Qt root directory. As an example, on my computer the flag is
set to “/home/ryan/Qt/5.5/gcc_64/”, though this will be different on
your machine. 5. On Linux run make in the terminal from the
build directory to build all the targets. On Windows the solution file
will be located in the build directory. Open the solution file in Visual
Studio and compile.
Introduction
This contains a C++ implementation of 3D Euler-Bernoulli beam element formulation. An analysis can be formulated in C++, through a command line interface via a configuration file (in JSON format), or using the graphical user interface.
Method 1: Using C++
An analysis consists of the fea::Job as well as any
boundary conditions (fea::BC), prescribed nodal forces
(fea::Force), ties (fea::Tie) and equation
constraints (fea::Equation). Ties to nodes together via a
linear springs between all translational and rotational degrees of
freedom, and equation constraints allow linear multi-point constraints
to be applied to the model. The fea::Options struct can be
used to request results of the analysis be written to disk as well as
modify various aspect of the analysis.
Forming the job
The job defines the nodal coordinates in (x, y, z)
space, the nodes that are connected to form beam elements, and the
elemental properties. The nodal coordinates are formed as a vector of
fea::Node’s where each node simply contains the
(x, y, z) coordinates of the point. An element contains the
2 nodal indices that are connected to form the element as well as the
associated properties of the element. The properties must define the
extensional stiffness, EA, bending stiffness parallel to
the local z-axis EIz, bending stiffness parallel to the
local y-axis EIy, the torsional stiffness, GJ,
and a vector pointing along the beam elements local y-axis. An example
forming a simple job with a single element is shown below.
// [form the node list
fea::Node node1, node2;
// place the first node at (0, 0, 0)
node1 << 0, 0, 0;
// place the second node at (1, 0, 0)
node2 << 1, 0, 0;
std::vector<fea::Node> node_list = {node1, node2};
// ]
// [ form the element list
// define the indices of the node list that form the element
unsigned int nn1 = 0;
unsigned int nn2 = 1;
// define the properties of the element
double EA = 1000.0;
double EIz = 100.0;
double EIy = 100.0;
double GJ = 200.0;
std::vector<double> normal_vec = {0.0, 0.0, 1.0};
fea::Props props(EA, EIz, EIy, GJ, normal_vec);
fea::Elem elem(nn1, nn2, props);
std::vector<fea::Elem> elem_list = {elem};
// ]
// a job is the combination of the node list and associated elements
fea::Job job(node_list, elem_list);Boundary conditions
Boundary conditions are applied by specifying the index of the node,
the degree of freedom, and the prescribed value. The index of the node
is simply the index the node occurs in the node list. The degree of
freedom can be defined using the fea::DOF enum or by
specifying the integer associated with the degree of freedom explicitly.
There are 6 degrees of freedom per node meaning valid integers
associated with degrees of freedom are between 0 and 5. The associations
for degrees of freedom are defined as
- 0 = displacement along the global x-axis.
- 1 = displacement along the global y-axis.
- 2 = displacement along the global z-axis.
- 3 = rotation about the global x-axis.
- 4 = rotation about the global y-axis.
- 5 = rotation about the global z-axis.
Continuing the example from above, we can fix all degrees of freedom of the node at the origin using the following code:
// fix all translational degrees of freedom using the fea::DOF enum
unsigned int nn1 = 0;
double value = 0.0;
fea::BC bc1(nn1, fea::DOF::DISPLACEMENT_X, value);
fea::BC bc2(nn1, fea::DOF::DISPLACEMENT_Y, value);
fea::BC bc3(nn1, fea::DOF::DISPLACEMENT_Z, value);
// fix all rotational degrees of freedom by explicitly using integer values
fea::BC bc4(nn1, 3, value); // x-axis rotation
fea::BC bc5(nn1, 4, value); // y-axis rotation
fea::BC bc6(nn1, 5, value); // z-axis rotation
// form the list of boundary conditions
// this vector will later be submitted to the
// fea::solve function to run an analysis
std::vector<fea::BC> bc_list = {bc1, bc2, bc3, bc4, bc5, bc6};Nodal forces
Nodal forces are assigned in the same manner as boundary conditions, i.e. using the node number, degree of freedom, and value. We can load our cantilever at the tip with the following:
// define the node index and value
unsigned int nn2 = 1;
double value = 1.0;
// create the force
fea::Force force(nn2, fea::DOF::DISPLACEMENT_Y, value);
// add to the list of forces for the analysis
std::vector<fea::Force> force_listOptions
By default submitting an analysis to the fea::solve
function will not save the results. The outputs must be requested using
the fea::Options struct. Using the appropriate member
variables nodal displacements, nodal forces, and the forces associated
with ties can be saved to a CSV file. The name of the file the output is
saved to is also set in the options as well as the delimiter used when
writing the data to disk. Additionally, the fea::Options
struct has the ability to set the epsilon value on nodal forces and
displacements. After the analysis if the magnitude of the displacement
is below the epsilon value, it will be set to 0.0. The default is
1.0e-14. A summary of the analysis can be saved to a text
file using the save_report and report_filename
member variables of fea::Options. If the
verbose member is set to true informational
messages regarding the current step and time taken on previous steps of
the analysis will be written to std::cout. An example of
customizing the analysis with the options struct is shown below:
// create the default options
fea::Options opts;
// request nodal forces and displacements
opts.save_nodal_forces = true;
opts.save_nodal_displacements = true;
// set custom name for nodal forces output
opts.nodal_forces_filename = "cantilever_beam_forces.csv"
// increase tolerance on epsilon
opts.epsilon = 1.0e-12;
// have the program output status updates
opts.verbose = true;Solving
Once the analysis has been setup, it can be solved using the
fea::solve function. This functions takes as input the job,
boundary conditions, prescribed nodal forces, ties (discussed below),
and options. fea::solve will solve the analysis, save the
requested files, and return a summary of the analysis. The
fea::Summary object can return a report of the analysis in
the form of a string using the fea::Summary::fullReport()
function, and member variables fea::Summary::nodal_forces,
fea::Summary::nodal_displacements, and
fea::Summary::tie_forces contain the results of the
analysis.
// form an empty vector of ties since none were prescribed
std::vector<fea::Tie> tie_list;
// also create an empty list of equations as none were prescribed
std::vector<fea::Equation> eqn_list;
fea::Summary summary = fea::solve(job, node_list, elem_list, bc_list, force_list, tie_list, eqn_list, opts);
// print a report of the analysis
std::cout << summary.fullReport() << std::endl;Upon successful compilation the full report printed to the command line should resemble:
Finite Element Analysis Summary
Model parameters
Nodes : 2
Elements : 1
BCs : 6
Ties : 0
Forces : 0
Equations : 0
Total time 0ms
Assembly time : 0ms
Preprocessesing time : 0ms
Factorization time : 0ms
Linear solve time : 0ms
Forces solve time : 0ms
File save time : 0ms
Nodal displacements
Minimum : Node 0 DOF 0 Value 0.000
Maximum : Node 1 DOF 5 Value 0.005
Nodal Forces
Minimum : Node 0 DOF 1 Value -1.000
Maximum : Node 1 DOF 1 Value 1.000Ties
Ties are enforced by placing linear springs between all degrees of freedom for 2 nodes. To form a tie specify the 2 nodes that will be linked as well as the spring constants for translational and rotational degrees of freedom. All translational degrees of freedom will be assigned the same spring constant. The same is true for rotational degrees of freedom, although the spring constant does not have to be the same as that used for the translational DOFs. Commonly, ties are used to model non-rigid joints. To form a joint between 2 elements, introduce a redundant node at that location and use a tie to link the to nodes together. This essentially places a spring element between the two points of the specified stiffness.
// form the job with a redundant node at (1, 0, 0)
fea::Node node1, node2, node3, node4;
node1 << 0, 0, 0;
node2 << 1, 0, 0;
node3 << 1, 0, 0;
node4 << 2, 0, 0;
std::vector<fea::Node> node_list = {node1, node2, node3, node4};
// define the properties of the elements
double EA = 1000.0;
double EIz = 100.0;
double EIy = 100.0;
double GJ = 200.0;
std::vector<double> normal_vec = {0.0, 0.0, 1.0};
fea::Props props(EA, EIz, EIy, GJ, normal_vec);
// constuct element list
fea::Elem elem1(0, 1, props);
fea::Elem elem2(2, 3, props);
std::vector<fea::Elem> elem_list = {elem};
// create the job
fea::Job job(node_list, elem_list);
// create the tie between node2 and node3
unsigned int nn1 = 1; // i.e. the second node in the node list
unsigned int nn2 = 2; // i.e. the third node in the node list
// define the spring constant for x, y, and z translational DOFs
double lmult = 100.0;
// define the spring constant for x, y, and z rotational DOFs
double rmult = 100.0;
// form the tie
fea::Tie tie1(nn1, nn2, lmult, rmult);
// add to list of ties
std::vector<fea::Tie> tie_list = {tie1};Equations
Equations are linear multi-point constraints that are applied to
nodal degrees of freedom. Each equation is composed of a list of terms
that sum to zero, e.g. t1 + t2 + t3 ... = 0, where
tn is the nth term. Each term specifies the
node number, degree of freedom and coefficient. The node number and
degree of freedom specify which nodal variable (either nodal
displacement or rotation) is involved with the equation constraint, and
coefficient is multiplied by the specified nodal variable when forming
the equation. Note, the equation sums to zero, so in order to specify
that 2 nodal degrees of freedom are equal their coefficients should be
equal and opposite.
// Create an empty equation
fea::Equation eqn;
// Stipulate that the x and y displacement for the first node must be equal
unsigned int node_number = 0;
eqn.terms.push_back(fea::Equation::Term(node_number, fea::DOF::DISPLACEMENT_X, 1.0));
eqn.terms.push_back(fea::Equation::Term(node_number, fea::DOF::DISPLACEMENT_Y, -1.0);Method 2: Using the command line interface
After using CMake to build the targets, an executable will be created
that provide a command line interface (CLI) to the beam element code.
Once in the build directory, navigate to the bin folder
containing fea_cmd. running ./fea_cmd -h from the terminal
will show the help documentation for the program. The CLI expects the
-c flag to be set and point to the config file for the
current analysis. A config file is a JSON document that contains key,
value pairs pointing to the nodes, elements, properties, and other
analysis options. An example is shown below.
{
"nodes" : "path/to/nodes.csv",
"elems" : "path/to/elems.csv",
"props" : "path/to/props.csv",
"bcs" : "path/to/bcs.csv",
"forces" : "path/to/forces.csv",
"ties" : "path/to/ties.csv",
"equations" : "path/to/equations.csv",
"options" : {
"epsilon" : 1.0E-14,
"csv_delimiter" : ",",
"csv_precision" : 8,
"save_nodal_forces" : true,
"save_nodal_displacements" : true,
"save_tie_forces" : true,
"save_report" : true,
"nodal_forces_filename" : "nodal_forces.csv",
"nodal_displacements_filename" : "nodal_displacements.csv",
"tie_forces_filename" : "tie_forces.csv",
"report_filename" : "report.txt",
"verbose" : true
}
}The use of a JSON document avoids the need to set each of these options using command line options, which can become tedious when running multiple jobs. The “nodes”, “elems”, and “props” keys are required. Keys “bcs”, “forces”, “ties” and “equations” are optional–if not provided the analysis will assume none were prescribed. If the “options” key is not provided the analysis will run with the default options. Any of all of the “options” keys presented above can be used to customize the analysis. If a key is not provided the default value is used in its place. See the Formatting CSV Files section below for how the CSV files should be created.
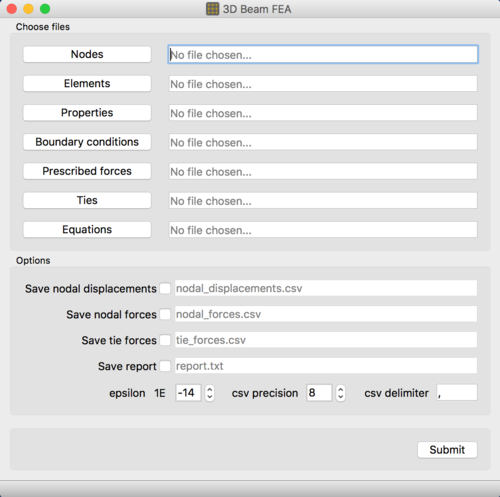
Method 3: Using the GUI
A simple graphical user interface can be used to set up an analysis.
Internally, the GUI creates the JSON file used by the CLI (see above)
without the need to write the file by hand. The program then saves a
temporary configuration file and submits it to the command line
application. This requires that the command line application has been
compiled and is located in the same directory as the GUI. To open the
GUI navigate to the build folder and open the fea_gui executable located
in the bin directory. The first set of buttons allows the
path to the CSV files to be set, and the second set of controls
customizes the options. Once the files and options have been configured,
clicking the submit button will run the analysis.
Formatting CSV files
All CSV file must be comma delimited with no spaces between values,
i.e. one row of the nodal coordinates file might resemble
1.0,2.0,3.0. The file indicated by the value of “nodes”
should be in the format:
x1,y1,z1
x2,y2,z2
...
...
...
xN,yN,zNwhere each entry is a double and every line must have 3 entries for
the x,y,z position. The “elems” file contains (only) the
node indices:
el1_node_num_1,el1_node_num_2
el2_node_num_1,el2_node_num_2
...
...
...
elN_node_num_1,elN_node_num_2where each entry is an integer and must have 2 nodal indices defining the connectivity of the element. Elemental properties are defined in the “props” file as:
el1_EA,el1_EIz,el1_EIy,el1_GJ,el1_nvec_x_comp,el1_nvec_y_comp,el1_nvec_z_comp
el2_EA,el2_EIz,el2_EIy,el2_GJ,el2_nvec_x_comp,el2_nvec_y_comp,el2_nvec_z_comp
...
...
...
elN_EA,elN_EIz,elN_EIy,elN_GJ,elN_nvec_x_comp,elN_nvec_y_comp,elN_nvec_z_compwhere each entry is a double and each line has 7 entries. The “bcs” and “forces” CSV files have the same format as each other. Each line specifies the node number, degree of freedom, and value:
bc1_node_num,bc1_dof,bc1_value
bc2_node_num,bc2_dof,bc2_value
...
...
...
bcN_node_num,bcN_dof,bcN_valuewhere the node number is the index of the node in the node list (integer), the DOF is the degree of freedom constrained (integer between 0 and 5), and value is the value to hold the degree of freedom at relative to the starting position (double). The “ties” CSV file is specified using the format:
tie1_node_num1,tie1_node_num2,tie1_lmult,tie1_rmult
tie1_node_num1,tie1_node_num2,tie1_lmult,tie1_rmult
...
...
...
tieN_node_num1,tieN_node_num2,tieN_lmult,tieN_rmultwhere lmult is the spring constant for the translational
degrees of freedom and rmult is the spring constant for the
rotational degrees of freedom. Equation constraints are specified by a
series of 3 items (representing a single term) repeated until the
desired number of terms are created. Each term is defined by the node
index, degree of freedom for the specified node, and the coefficient
that will multiply the nodal degree of freedom. For example a single
equation constraint that specifies that the x and y displacements for
the first node must remain equal is given by:
0,0,1,0,1,-1in general the equations CSV file will be resemble:
eq1_term1_node,eq1_term1_dof,eq1_term1_coeff,...
eq2_term1_node,eq2_term1_dof,eq2_term1_coeff,...
...
...
...
eqN_term1_node,eqN_term1_dof,eqN_term1_coeff,...Contact
- Ryan Latture (ryan.latture@gmail.com)